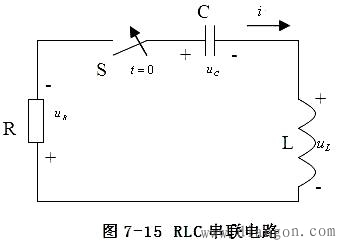
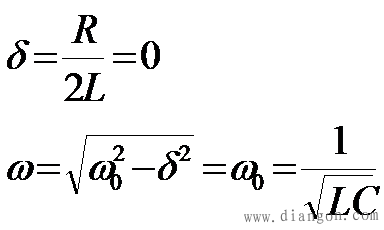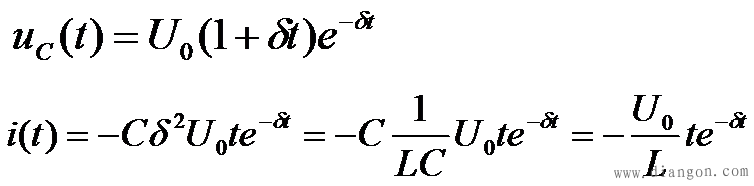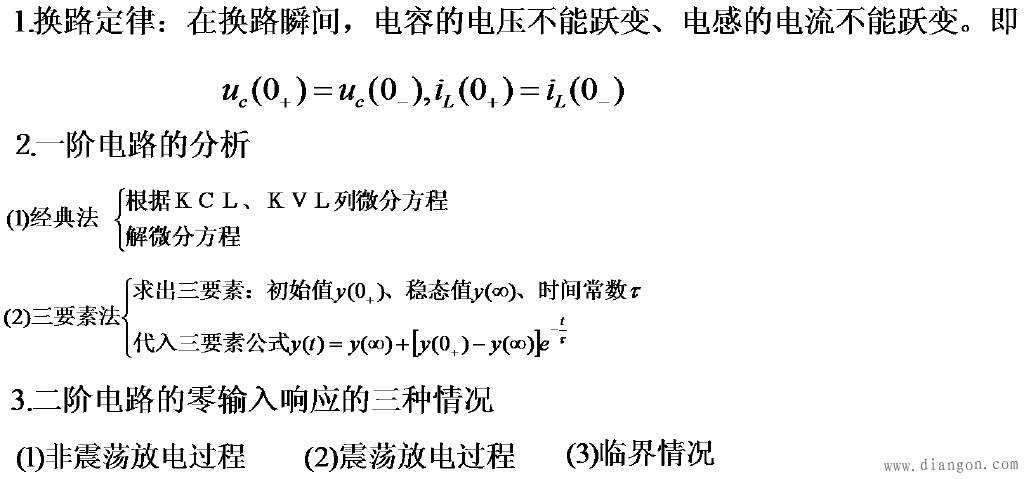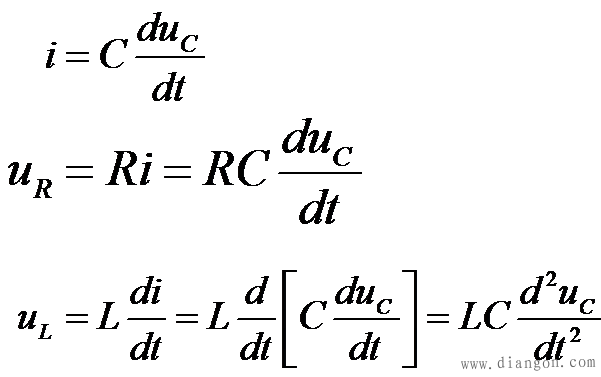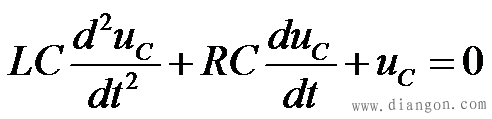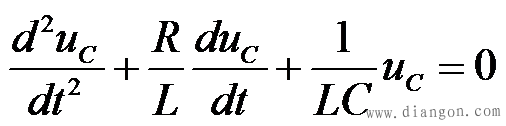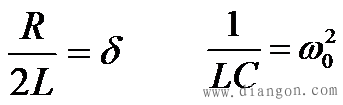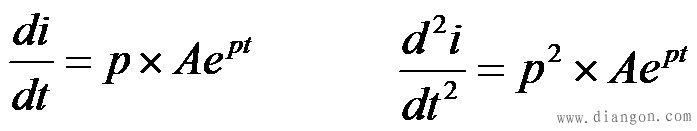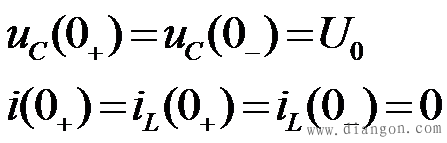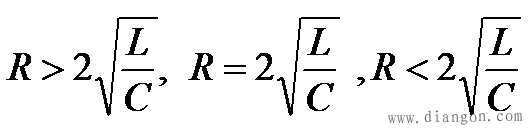1、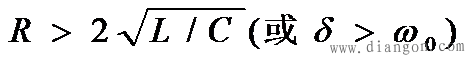 非振荡放电过程 非振荡放电过程在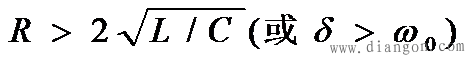 的情况下p1、p2 、为两个不等的负实根,不妨设 的情况下p1、p2 、为两个不等的负实根,不妨设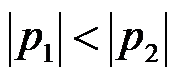 ,解电路方程可得到 ,解电路方程可得到 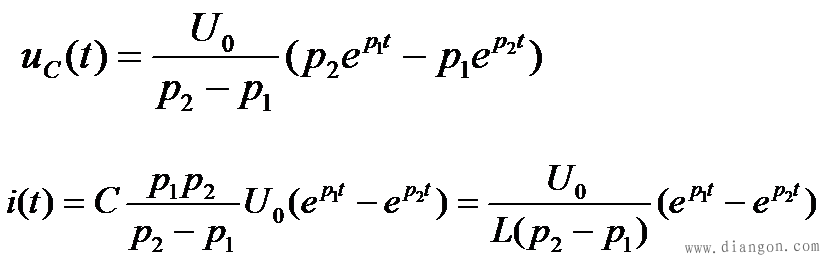
电容电压的变化曲线如图7-16(a)所示,放电电流的变化曲线如图7-16(b)所示。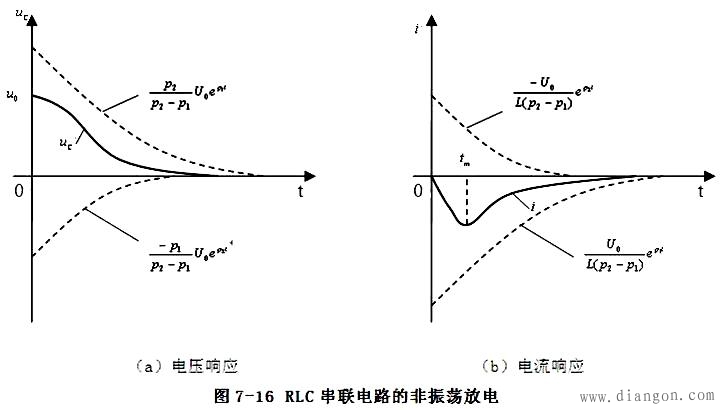
上述放电过程中,电容一直处于放电状态,并没有能量从电感向电容充电的过程,所以称为非振荡放电。从物理意义上来说,这是电容通过电阻和电感的放电过程。起初,电容放出的能量一部份转化为磁场能量,另一部分被电阻消耗。在t=tm时电流达到*大值后,磁场能量不再增加,并且电感线圈开始释放能量,故在t>tm后,电容和电感同时放出能量供电阻消耗,直到电场储能与磁场储能被电阻耗尽,放电结束。在这个过渡过程中,电容器中电场储能是单调减小的,没有振荡。这是因为电阻过大,电阻耗能迅速造成的,所以,这是一种过阻尼情况。 2、 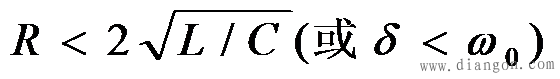 振荡放电过程 振荡放电过程在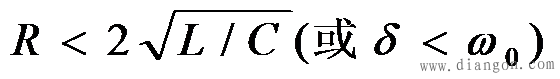 的情况下,p1 、p2 为一对共轭复根,则解电路方程可得到幅度衰减的正弦振荡解: 的情况下,p1 、p2 为一对共轭复根,则解电路方程可得到幅度衰减的正弦振荡解: 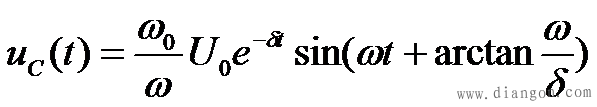
式中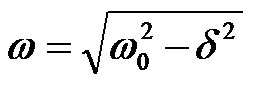 ,而电流 ,而电流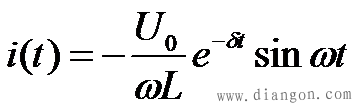 电容电压 、电流 的变化曲线如图7-18所示。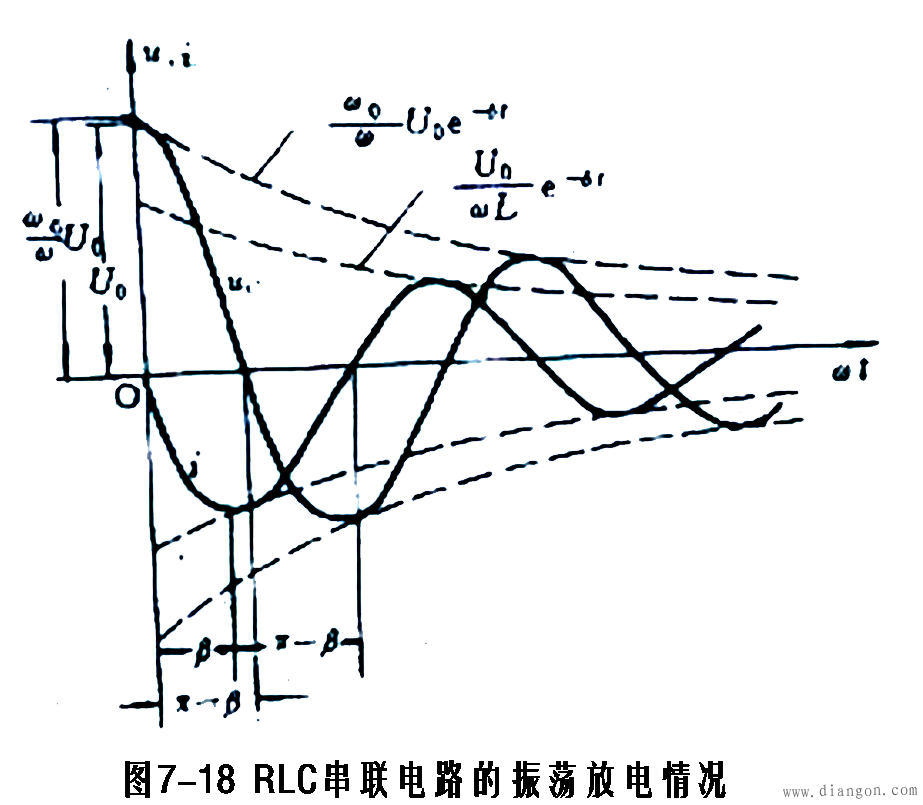 电流 i(t)都是振幅按指数规律衰减的正弦函数,所以这种放电过程称为振荡放电。这种振荡由于电阻较小,耗能较慢,所以电感和电容之间进行往复的能量交换,从而形成了振荡。由于电阻的存在,所以是衰减振荡,也称欠阻尼振荡。 电流 i(t)都是振幅按指数规律衰减的正弦函数,所以这种放电过程称为振荡放电。这种振荡由于电阻较小,耗能较慢,所以电感和电容之间进行往复的能量交换,从而形成了振荡。由于电阻的存在,所以是衰减振荡,也称欠阻尼振荡。 如果电路的电阻R=0,则衰减系数δ及回路振荡角频率ω分别为 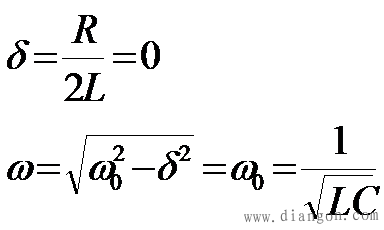
则 u(t)和i(t) 都是不衰减的正弦量,是一个等幅振荡的过程。实质上这是电容储能和电感储能之间反复转化而没有消耗的过程。因为没有能量损耗,所以振荡将一直进行下去。 3、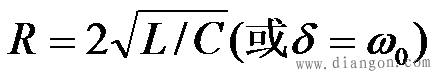 临界情况 临界情况正弦激励下的一阶电路,稳态响应也是正弦量。可以用相量法求得。时间常数是电路本身的参数,与激励无关。计算方法与上面相同。
在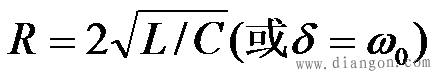 的情况下,p1 、p2 为两个相等的负实根,则电路方程的解为 的情况下,p1 、p2 为两个相等的负实根,则电路方程的解为 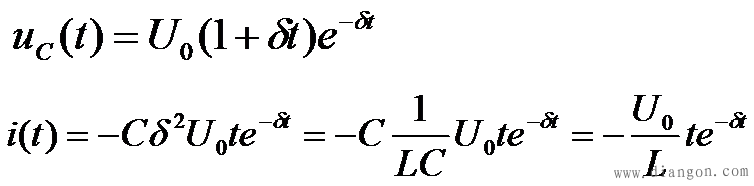
可以看到,u(c)变化情况是从 U0开始,保持正值,逐渐衰减到零;i是从零开始,保持负值,*后为零。这个过程也是非振荡的。u(c)和i的曲线与图7-16非常相似。 这一情况下的放电过程是振荡与非振荡过程的分界线,所以也称为临界阻尼情况,而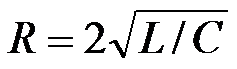 则称为RLC串联电路的临界电阻。 则称为RLC串联电路的临界电阻。 重点串联
| 



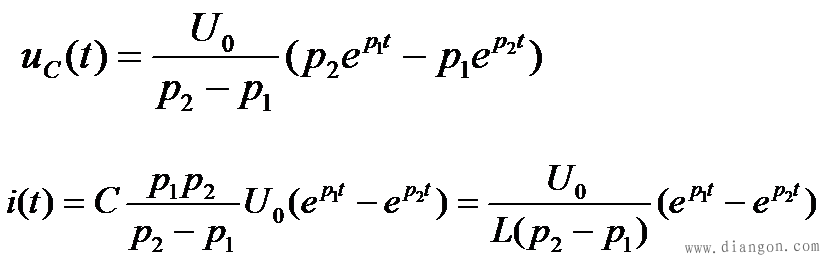

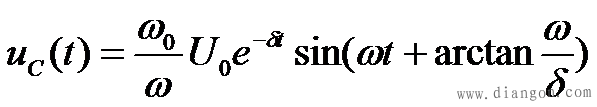
 电流 i(t)都是振幅按指数规律衰减的正弦函数,所以这种放电过程称为振荡放电。这种振荡由于电阻较小,耗能较慢,所以电感和电容之间进行往复的能量交换,从而形成了振荡。由于电阻的存在,所以是衰减振荡,也称欠阻尼振荡。
电流 i(t)都是振幅按指数规律衰减的正弦函数,所以这种放电过程称为振荡放电。这种振荡由于电阻较小,耗能较慢,所以电感和电容之间进行往复的能量交换,从而形成了振荡。由于电阻的存在,所以是衰减振荡,也称欠阻尼振荡。