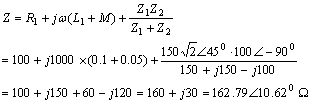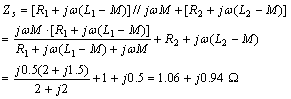SIMATIC ET 200pro 是一种采用高防护等级 IP65/66/67 的新型模块式 I/O 系统，用于无电控柜本地应用。防护等级为 IP65 的 ET 200pro 电机起动器是 ET 200pro 不可分割的一部分。
ET 200pro 电机起动器：安装在宽模块架上的隔离模块、标准型起动器和高性能型起动器
在环形磁芯上用漆包线绕一个耦合电感，初级60匝，次级30匝，如图所示。
在环形磁芯上用漆包线绕一个耦合电感，初级60匝，次级30匝，如图所示。 在初级加上999kHz的正弦信号，用示波器观察到正弦波形。
在耦合电感的次级上，可以观察到正弦波形，其幅度约为初级电压的一半。
用双踪示波器可以同时观察耦合电感初级和次级线圈上的正弦电压波形，它们的相位是相同的。
当我们改变次级线圈的绕向时，耦合电感初级和次级线圈上电压波形的相位是相反的。
为了区别这两种情况，需确定耦合电感的同名端，图示耦合电感线圈的两个红色（或绿色）端钮是一对同名端。当初次级电压参考方向的正极都在同名端时，它们的相位相同。 |
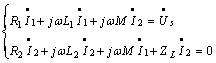
令
，是原边电路阻抗，
，是副边电路阻抗，其中
是负载阻抗，
是互感阻抗。则
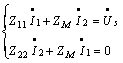
解得：
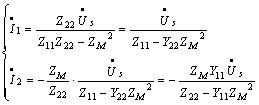
式中，
，是原边电路导纳，
，是副边电路导纳。
原边电路的输入阻抗为
一、耦合电感元件的相量模型 | |||
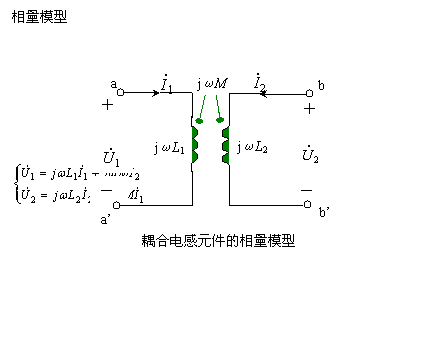 二、耦合电感的去耦等效 两个线圈之间存在磁耦合，每个线圈的电压不仅与本线圈的电流变化率有关，而且与另一个线圈的电流变化率有关，其伏安关系中的正、负号又取决于同名端的位置及电压、电流的参考方向等。所以，对含有耦合电感的电路的分析就相对比较复杂。 耦合电感在一定的条件下存在去耦等效电路。对某些特定结构的耦合电感作去耦等效，找出其相应的去耦等效电路，使电路的分析得以简化。 1、串联的去耦等效 | |||
 | |||
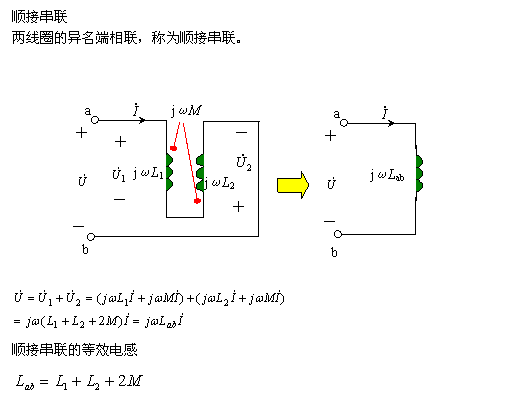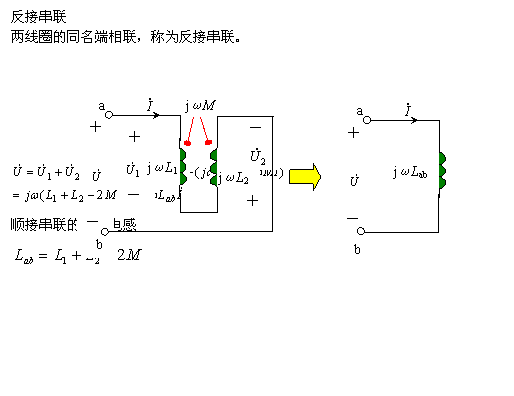 2、并联的去耦等效 | |||
 | |||
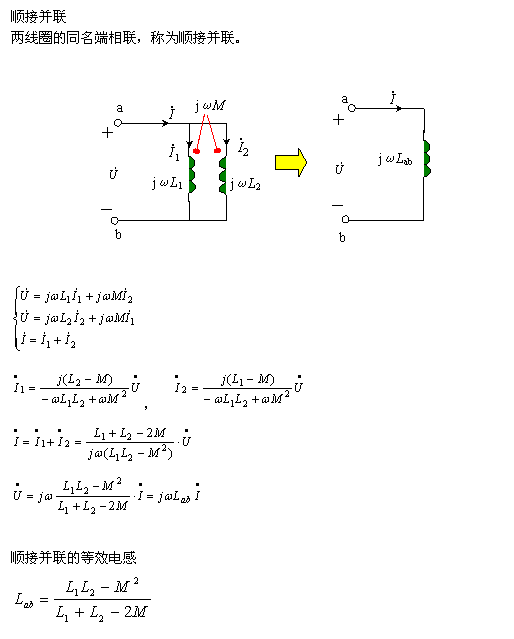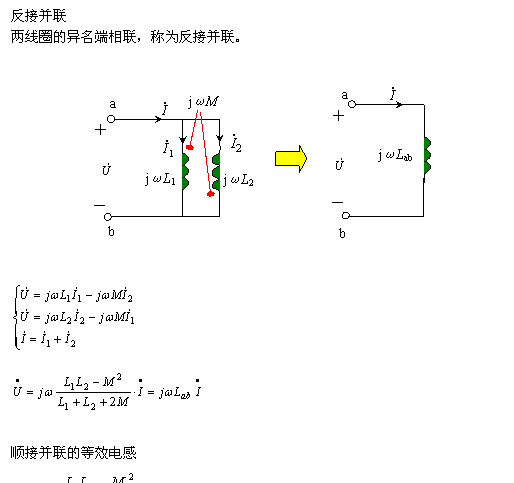 3、Y形连接的去耦等效 | |||
 | |||
 | |||
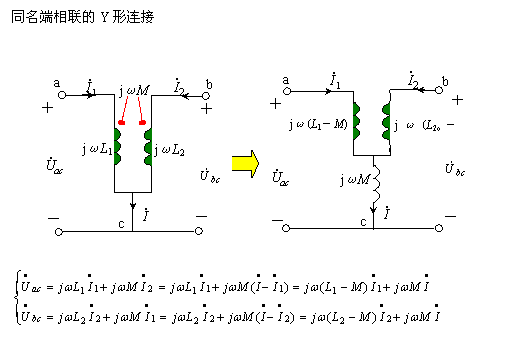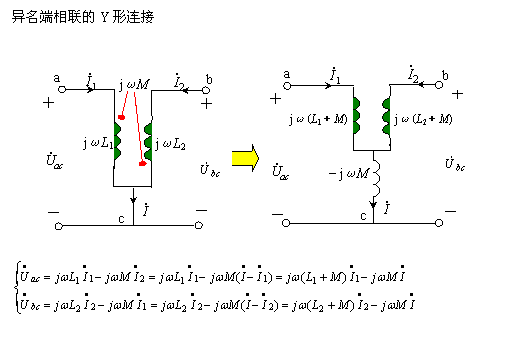三、含有耦合电感的正弦稳态电路分析 含有耦合电感的正弦稳态电路的分析，依然采用相量法，只是要注意耦合电感的特点。为了使分析和计算简化，如果能去耦等效的，那么先对它去耦等效，得到去耦后等效电路。这样电路中的就不存在耦合电感，只有自感，等效后的电路与第7章的正弦稳态电路并无区别，当然其分析的方法也就一样；如果耦合电感不能去耦等效，那么，就根据耦合电感的基本概念和同名端的位置，列写电路方程，并进行计算。 例8.2-1 图8.2-1（a）所示的正弦稳态电路中，电压源 | |||
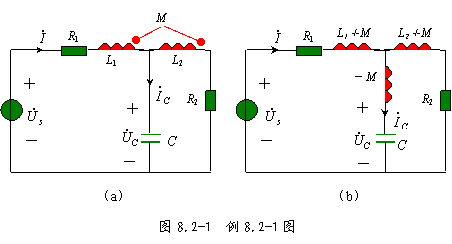 解：图8.2-7（a）电路的耦合电感是异名端相联，作Y形去耦等效，其等效电路如图8.2-7（b）所示。 电阻R2和电感（L2＋M）串联后的等效阻抗为
电感（－M）和电容C串联后的等效阻抗为
则电路的总等效阻抗为
所以，
由分流公式，得电容电流为
则
因此，电容电压为
例8.2-2 电路如图8.2-8（a）所示，已知 | |||
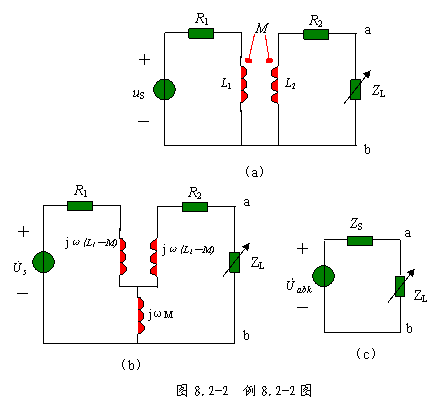 解：对图8.2-8（a）电路作去耦等效，得图8.2-8（b）所示的等效电路。 图8.2-8（b）中，电压源
再求戴维南等效阻抗
所以，用戴维南定理等效后的等效电路如图8.2-8（c）所示。 由*大功率传输定理，当负载阻抗与等效内阻抗共轭匹配时，负载获得*大功率，则负载阻抗为
*大功率为
| |||
四、空心变压器 空心变压器是绕在非铁磁芯上的两个耦合线圈。其中，一个线圈作为输入，接入电源或信号源，称为原边电路或初级电路（primary circuit），另一个线圈作为输出，接入负载，称为副边电路或次级电路（secondary circuit）。 | |||
 | |||
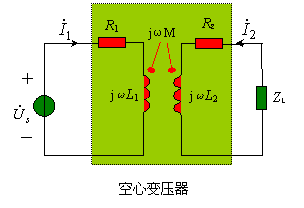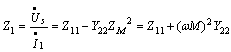
空心变压器的原边输入阻抗中，除了原边本身的阻抗 由于 | |||
，
，
，
，
，
，
，
。求电容C上的电压
。
，
，
，电感
，
，互感
，负载
，用戴维南定理求a、b两端左边电路的等效电路。先求a、b两端的开路电压
，由于a、b两端开路，电阻R2和感抗jω(L2－M)上没有电压，那么，开路电压
就等于感抗jωM上的电压，由分压公式得
，将电压源短路，则
外，还包含了由互感和副边电路导纳决定的阻抗，即
，它是反映副边电路通过互感对原边电路产生影响的一个阻抗，称为反射阻抗。
，这就说明，如果副边电路阻抗
是感性的，则反映到原边输入阻抗中的反射阻抗是容性的；反之，如果副边电路阻抗